پاسخ تمرینهای صفحه ۱۳ کتاب ریاضی پایه ششم
**فعالیت صفحه ۱۳**
در این فعالیت، با استفاده از شکلهای داده شده، باید اندازهی زاویههای خواسته شده را پیدا کنید. به این نکات توجه کنید:
* مجموع زاویههای داخلی یک مثلث همیشه ۱۸۰ درجه است.
* زاویهی نیمخط (زاویهی راست) ۹۰ درجه است.
* وقتی دو خط به هم برخورد میکنند، زاویههای روبرو به هم (زاویههای متقابل به رأس) با هم برابرند.
با در نظر گرفتن این قوانین و با توجه به اندازههایی که در شکل مشخص شده است، میتوانید اندازهی هر زاویهی مجهول را به دست آورید.
**کار در کلاس صفحه ۱۳**
در این بخش نیز باید اندازهی زاویههای نامشده را حساب کنید. برای حل این مسئله به این موارد دقت کنید:
* در یک مثلث، اگر اندازهی دو زاویه را داشته باشیم، اندازهی زاویهی سوم از تفریق مجموع آن دو زاویه از ۱۸۰ درجه به دست میآید.
* زاویهی خارجی در یک مثلث با مجموع دو زاویهی داخلی غیر مجاورش برابر است.
با کمک این قواعد و با نگاه دقیق به شکل، میتوانید جواب هر قسمت را پیدا کنید.

**عنوان:** درس سوم: بخشپذیری | **نوع محتوا:** راهنمای گامبهگام | **پایه:** ششم دبستان
در این درس با مفهوم بخشپذیری آشنا میشویم. بخشپذیری به این معناست که وقتی یک عدد را بر عدد دیگری تقسیم میکنیم، باقیمانده تقسیم صفر شود.
برای مثال، عدد ۱۰ بر ۲ بخشپذیر است، زیرا ۱۰ تقسیم بر ۲ میشود ۵ و باقیمانده صفر میشود. اما عدد ۱۰ بر ۳ بخشپذیر نیست، زیرا باقیمانده آن ۱ میشود.
در ادامه، با قواعد بخشپذیری بر اعداد مختلف مانند ۲، ۳، ۵، ۶، ۹ و ۱۰ آشنا خواهیم شد. این قواعد به ما کمک میکنند تا خیلی سریع و بدون انجام تقسیم کامل، متوجه شویم که یک عدد بر عدد دیگر بخشپذیر است یا خیر.
یادگیری این قواعد حل بسیاری از مسائل ریاضی را برای ما آسانتر میکند.
گام به گام ریاضی ششم صفحه 13 با جواب
انتخاب بخش مورد نظر:
حل تمرین صفحه ۱۳ ریاضی ششم
پاسخ سوالات کلاسی صفحه ۱۳ ریاضی ششم
حل فعالیت صفحه ۱۳ ریاضی ششم
پاسخ تمرینات صفحه ۱۴ ریاضی ششم
در این قسمت پاسخ کامل صفحه ۱۳ کتاب ریاضی پایه ششم ابتدایی قرار داده شده است. در پایان مطلب میتوانید دیدگاه و پیشنهادات خود را با ما در میان بگذارید. همچنین توصیه میکنیم برای مطالعه مطالب بیشتر، از بخش فصل اول ریاضی ششم بازدید نمایید.
کار در کلاس صفحه ۱۳ ریاضی ششم
اعدادی را که بر دو تقسیم میشوند، دور آنها خط بکشید.
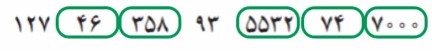
اعدادی را که بر ۵ بخشپذیر هستند، مشخص کنید و دور آنها خط بکشید.
![]()
با استفاده از کارتهای اعداد ۹، ۰ و ۵، اعداد سهرقمی زیر را میتوان ساخت:
الف) عددی که بر ۲ بخشپذیر باشد:
۹۵۰ – ۵۹۰
ب) عددی که بر ۵ بخشپذیر باشد:
۹۵۰ – ۹۰۵
پ) عددی که بر ۵ بخشپذیر باشد، اما بر ۲ بخشپذیر نباشد:
۹۰۵
ت) عددی که نه بر ۲ و نه بر ۵ بخشپذیر باشد:
۵۰۹

۴- جای خالی را با عدد مناسب پر کنید.
– بزرگترین عدد سه رقمی که بر ۲ تقسیم میشود، عدد ۹۹۸ است.
– کوچکترین عدد سه رقمی که بر ۵ تقسیم میشود، عدد ۱۰۰ است.
۵- دور عددهایی که هم بر ۲ و هم بر ۵ بخش پذیر هستند، خط بکشید.
![]()
– آیا اعدادی که انتخاب کردید بر ۱۰ تقسیم میشوند؟
پاسخ: بله
– رقم یکان این اعداد چند است؟
پاسخ: صفر
– آیا میتوانید عددی نام ببرید که بر ۱۰ بخشپذیر باشد، ولی رقم یکان آن صفر نباشد؟
پاسخ: خیر
۶– چرا اعدادی که بر ۱۰ تقسیم میشوند، همیشه رقم یکانشان صفر است؟
پاسخ: زیرا همهی این اعداد از ترکیب یک یا چند دستهی ۱۰ تایی، ۱۰۰ تایی، ۱۰۰۰ تایی و… تشکیل شدهاند.
جواب فعالیت صفحه ۱۳ ریاضی ششم
اگر این تصویرها نشاندهنده کلوچههای داخل یک بسته باشند،
وقتی یک بسته صدتایی از این کلوچهها را به سه بخش برابر تقسیم کنیم،
چه تعداد کلوچه باقی میماند؟
پاسخ: یک کلوچه.
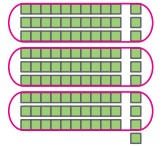
وقتی یک بسته دهتایی کلوچه را میخواهیم به سه بخش کاملاً مساوی تقسیم کنیم، چه اتفاقی میافتد؟
پاسخ: یک کلوچه اضافه میآید.
![]()
پس وقتی هر بستهی صدتایی و دهتایی را بر ۳ تقسیم میکنیم، باقیمانده برابر با ۱ خواهد بود.
– اگر ۲ بستهی صدتایی را بر ۳ تقسیم کنیم، باقیمانده چقدر است؟
پاسخ: ۲
– حالا اگر ۲ بستهی دهتایی را بر ۳ تقسیم کنیم، باقیمانده چقدر میشود؟
پاسخ: ۲
– اگر هر بستهی صدتایی کلوچه را به ۹ قسمت مساوی تقسیم کنیم، چند کلوچه باقی میماند؟ با کشیدن یک خط نشان دهید.
پاسخ: یکی
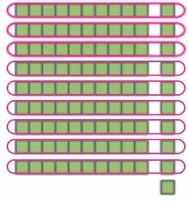
وقتی یک بسته دهتایی کلوچه را میخواهیم به ۹ قسمت مساوی تقسیم کنیم، چه اتفاقی میافتد؟
پاسخ: یک عدد از آنها باقی میماند.
![]()
پس وقتی هر دستهی صدتایی یا دهتایی را بر ۹ تقسیم کنیم، باقیمانده برابر با …۱… خواهد بود.
– اگر ۲ دستهی صدتایی را بر ۹ تقسیم کنیم، باقیمانده چقدر میشود؟
پاسخ: ۲
– در مورد ۲ دستهی دهتایی چطور؟
پاسخ: ۲
– اگر ۳ دستهی صدتایی را بر ۹ تقسیم کنیم، باقیمانده چقدر است؟
پاسخ: ۳
– در مورد ۳ دستهی دهتایی چطور؟
پاسخ: ۳
جواب صفحه ۱۴ ریاضی ششم
یک چاپخانه قصد دارد ۲۸۲ جلد کتاب را صحافی کند. مدیر چاپخانه میخواهد این کتابها را به طور مساوی بین سه کارگر تقسیم کند. آیا پس از تقسیم، کتابی باقی میماند؟
پاسخ: خیر
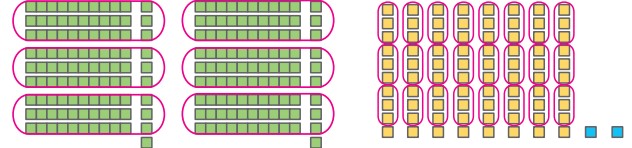
عدد ۲۸۲ نشان میدهد که …۲… تا صدتایی، …۸… تا دهتایی و …۲… تا یکی داریم.
با نگاه به شکل، وقتی میخواهیم صدتاییها را به سه بخش برابر تقسیم کنیم، چند کتاب باقی میماند؟
پاسخ: ۲ کتاب
در تقسیم دهتاییها چطور؟
پاسخ: ۸ کتاب
همه کتابها به سه بخش مساوی تقسیم شدهاند، به جز:
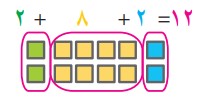
بین اعداد ۲ و ۸ و ۲ که در کنار هم عدد ۲۸۲ را میسازند، چه رابطهای وجود دارد؟
پاسخ: اگر این سه رقم را با هم جمع کنیم (۲+۸+۲)، حاصل جمع آنها با مجموع ارقام عدد ۲۸۲ برابر است.
– آیا راه سادهای برای تشخیص اینکه عدد ۲۸۲ بر ۳ بخشپذیر است، میشناسید؟
پاسخ:
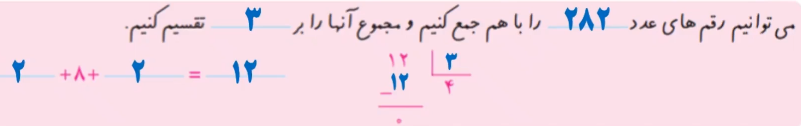
اگر مجموع رقمهای عدد ۲۸۲ بر ۳ بخشپذیر باشد، پس خود عدد ۲۸۲ نیز بر ۳ بخشپذیر خواهد بود.
آیا هنگام تقسیم کتابها بین سه نفر برای صحافی، کتابی باقی میماند؟
پاسخ: خیر.
حال اگر پس از صحافی بخواهیم کتابها را بهطور مساوی در ۹ کارتن قرار دهیم، آیا کتابی باقی خواهد ماند؟
با توجه به محاسبات انجامشده، از تقسیم صدتاییها بر ۹، عدد ۲ بهدست میآید و از تقسیم دهتاییها بر ۹ نیز عدد ۸ باقی میماند.
بنابراین، همهٔ کتابها بهطور مساوی بین ۹ کارتن تقسیم میشوند به جز:
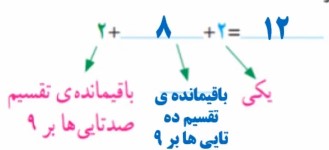
اگر عدد …۱۲… را بر ۹ تقسیم کنیم، باقیمانده برابر با …۳… خواهد بود. بنابراین، …۳… کتاب باقی میماند.
آیا میتوان از روشی که برای تشخیص بخشپذیری اعداد بر ۳ گفته شد، برای تشخیص بخشپذیری بر ۹ نیز استفاده کرد؟
پاسخ: بله
